挖掘数据与表达,是时候提升数据分析水平了
看见别人看不见的价值,用图表武装思想。

使用上篇讲述的常规的数据分析手段,能够帮助我们快速对数据进行规整和剖析,进而总结出数字反映的客观事实。我们常提到的数据统计及分析工作,大部分止步于此。
然而是否有可能对数据进行更深层次的挖掘,去寻找一些不那么显著可见的事实背后隐藏的规律,甚至是一些猜想呢?
答案是肯定的。
为了达成该目的,我们需要借助一系列机器学习的算法,这也是本篇的重点内容之一。

在完成全部分析形成结论后,若要精益求精就无法绕过最终的图表美化工作,即数据可视化,良好的表达呈现有助于观众更好的理解你的观点。
产品需要考虑表现层的用户体验,数据报告亦是如此。
因此,本文最后的篇幅会留给数据可视化。
回顾一下数据分析的5个步骤:
- 明确目标;
- 数据预处理;
- 特征分析;
- 算法建模;
- 数据表达。
上篇《 极简数据分析(上) – 10分钟掌握关键数据分析方法》 介绍了前3步,本篇开始进入到最后2个步骤。
算法建模
不少非技术出身的同学一听到算法建模、机器学习、大数据、人工智能等概念,就开始头大,实际上大可不必。
本文其实也是定位面向于非技术人员的,因此首先可能需要对相关的技术进行去魅。
什么是算法?
可以理解成算法是计算的方法或技巧,通过合适的算法对原始数据进行加工以得出结论,是我们解决问题的核心思路。
什么是数据挖掘?
顾名思义,是对并非浮于表面的信息进行深度研究,可能是可观察到的事实背后的规律或原因,也是我们想获取的知识。
什么是机器学习?
其目的是让机器可以通过学习,自主去解决问题,而并非执行一段代码内既定的任务。
而人工智能可能是最后我们追求的美好结果,不论是数据挖掘还是机器学习,都是在实现人工智能过程中的手段,虽然其实离真正的智能还相差甚远。
所以在数据分析范畴内对相关技术的应用,我们可以描述为:利用机器学习的相关算法进行数据挖掘,寻找数据事实背后的规律。
一个好消息是:算法在人工智能技术和高级语言经历了多年发展至今后,很多已经被封装成了独立的函数或类,可以直接调用,不少开发框架内也已经集成了大量的库或包,大大降低了机器学习的技术门槛,也因此让我们利用相关技术进行数据分析成为了可能。
机器学习主要分为监督学习和非监督学习,此外还有强化学习。
这里主要介绍监督学习和非监督学习。两者的区别主要在于是否有已知的训练集,即监督学习类似教学,告诉机器一些已经确定的输入条件(特征值)和输出结果(标签),然后由机器总结规律再运用到新样本中。而非监督学习类似自学,机器需要自己从全部样本中总结规律。
在数据分析过程中,根据分析目的和数据特征的不同,通常会进行3类分析:回归、分类、聚类。在每类分析中还包含了多种模型,接下来我们会介绍其中常用且有代表性的模型和实现方式。
1. 线性回归
线性回归可能是大家平时听到最多的模型了,其通常被应用在对连续变量的预测中。
线性回归会尝试在一些已知的自变量和因变量之间寻找到一种关系,通过拟合出最佳的回归线去表达这种关系,进而可以预测在回归线上其他点的数据。如根据下面左图的已知数据,拟合出右图的直线函数。

在Python中可直接调用sklearn库中的相关模型实现,简单的一元线性回归实例如下,多元线性回归的实现类似,但会有多个自变量,即输出的斜率值会有多个。
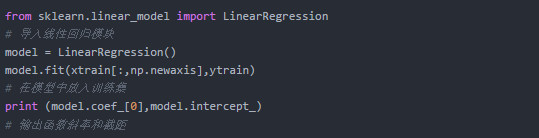
既然该模型是基于已知数据拟合得出的,就可能存在过拟合或欠拟合的可能,不论哪种都会使模型失去泛化的能力,很难去进行预测。
造成问题的最常见原因可能是训练样本量太少或者样本的维度太少。
sklearn库中也提供了一系列参数用于评价模型拟合水平,例如SSE(和方差)、MSE(均方差)、RMSE(均方根)、R-squre(确定系数)等。其中SSE、MSE和RMSE的逻辑类似,数值越接近0说明效果越好,R-squre取值范围在[0,1]之间,越接近1说明效果越好。
2. 聚类
聚类是非监督学习的代表,指的是根据样本间相似的特征进行分类的过程。聚类中的常用算法有K-Mean算法,是典型的基于距离的聚类算法,常以欧氏距离进行测量(不理解也不重要),更适合形状比较规则的类簇。
而有些聚类效果不规则,带狭长、拐弯(非凸样本集),则不适合用K-Mean算法,针对这种情况会使用密度聚类的算法,例如DBSCAN。下图可看出两种算法的聚类区别,对于形状不规则的聚集,DBSACN效果会更好。
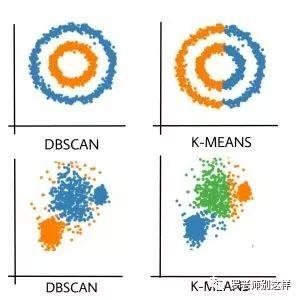
但大部分时候我们遇到的聚类情况还是比较规则的,也因此K-Mean仍是更常用的聚类算法。在K-Means算法的逻辑中,要注意2点:
- 需要事先给定类簇的数量,即聚类群的个数;
- 需要事先给定类簇初始的中心。
在Python中的实现和聚类效果如下:
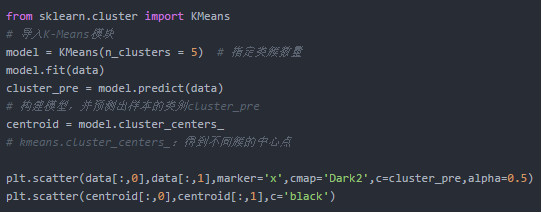
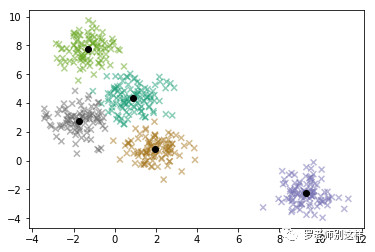
根据聚类结果,不仅可研究相似群体的规律,还可以找出与大众差异非常大的孤立点,这在例如风控行业中的应用非常普遍,孤立点很可能代表着一些刷单或有其他不良行为的恶意用户。
3. 分类
之所以把分类放在最后,是因为无论其重要性还是应用范围可能都是最高最广的。这是一种利用已知训练集来对模型进行训练,不断优化分类器的过程。
分类的算法也非常多,而且还有不少变种或衍生算法。我们只能列举一些最经典也是最普适的算法,例如朴素贝叶斯、决策树、随机森林、SVM(支持向量机)、遗传算法等。
接下来以非常简单的KNN算法为例,介绍分类的实现方式。KNN全称K-Nearest-Neighbors,其思路简单描述就是将待判断的样本放入已知训练结果中,观察样本和哪个群体的成员间最接近,就将其归为哪类。这次直接利用Python中的测试数据实现,该测试数据为判断3种花的类型,以及4个花的特征(萼片长度、萼片宽度、花瓣长度、花瓣宽度)。
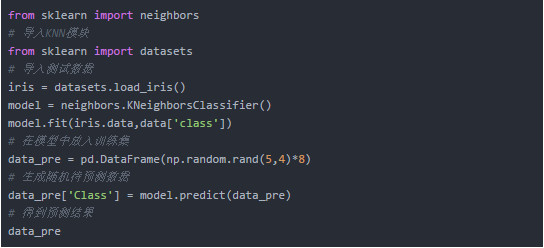
对随机数据的判断结果如下:
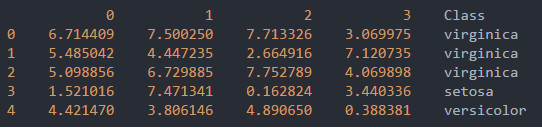
数据表达
终于来到最后一步,数据表达。数据分析最终要形成具有指导性的结论,结论一定是要给他人观看讲解的,因此良好的表达十分必要。
下图是一张经典的图表选择决策图,参考此图可以快速根据表达目的选择合适的图表进行可视化表达。
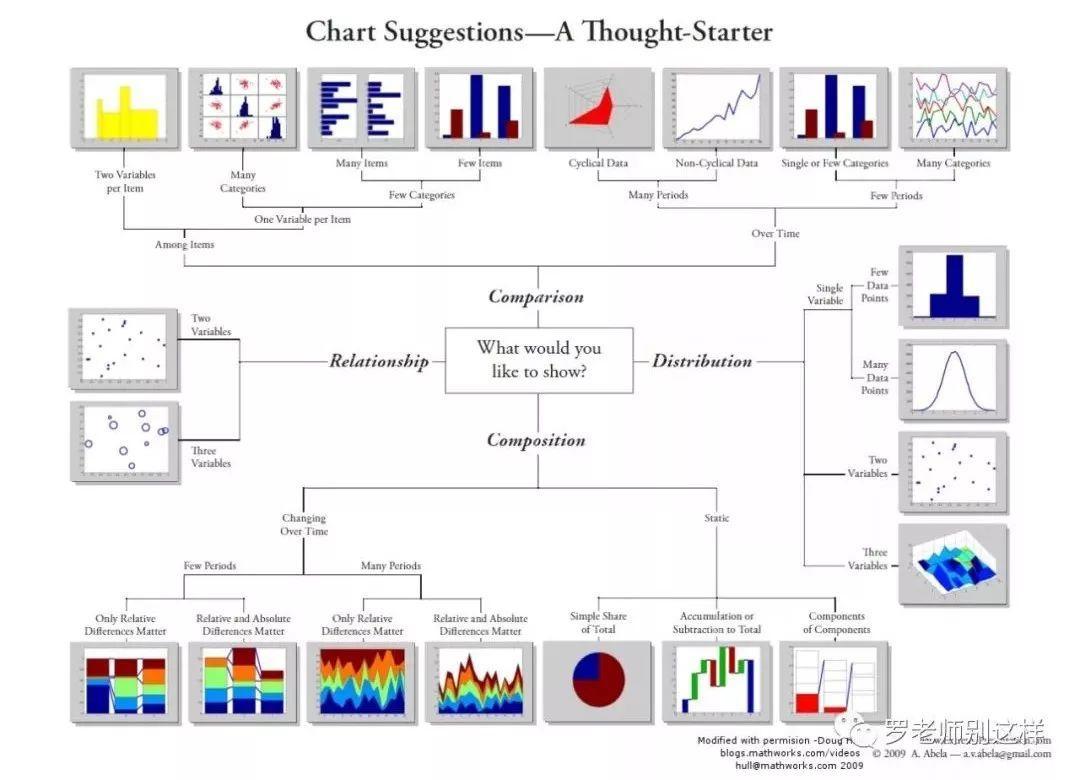
表达目的在图中主要分为4种:分布、对比、相关性、构成,并对应了不同的图表,相信在工作中绝大部分的数据表达需求都已经可以对号入座。
虽然图表并非信息量越大越好,表现形式越酷炫越好,但恰到好处的丰富程度和展现形式还是能更高效地提供更多有价值的信息,也确实比过于简单的图表更加专业。
因此接下来本文会展示一些包含更多细节和不同形式的图表并辅以解释,希望能够给你提供参考,带来启发。
1. 分布数据可视化
直方图+密度图:该组合可以很好的展示数据的整体分布趋势,密度图曲线是对分布趋势的拟合,可以调节拟合程度。还可以用线段代表具体样本,展示绝对分布情况。
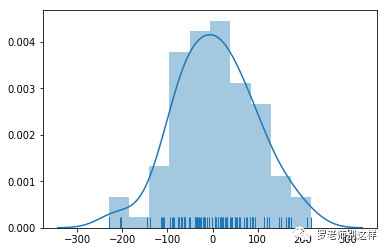
多维度密度图:通常是2个维度,例如表达地理位置的经纬度。
通过该密度图能反映数据的聚集情况,还可以在密度图基础上绘制散点图来标注出原始数据。看上去是不是很像地理课上学的等高线?
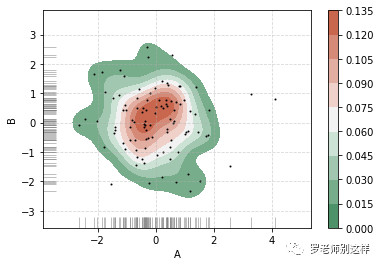
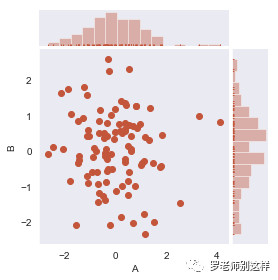
散点图:针对基础的散点图,我们可以在横轴坐标上辅以直方图或密度图以反映数据在单个维度上的分布情况。
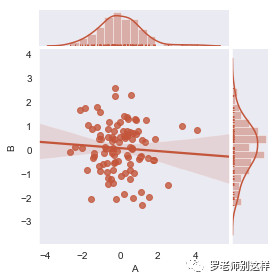
甚至还能运用前面讲到的线性回归,对数据进行回归分析,给出拟合结果和置信区间。
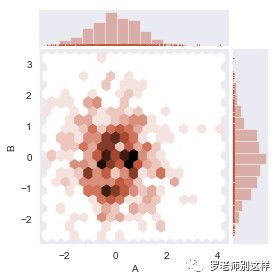
散点图的表达形式也不仅限于散点,还可以用类似蜂巢的六边形,根据颜色深浅可以看出分布情况。
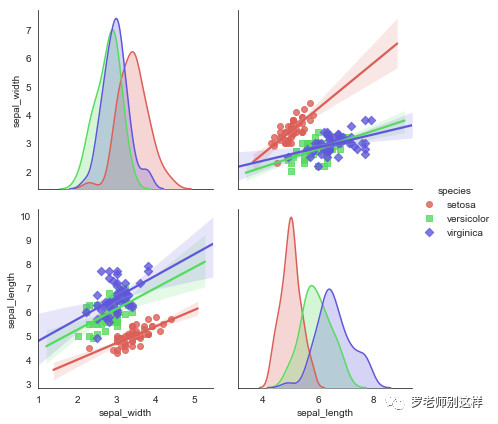
散点图矩阵:在上篇已经有介绍过散点图矩阵了,利用该矩阵可快速对样本间的关系进行初判。而在数据表达阶段给出的矩阵是已经完成判断后的结果展示,表达的形式也会更丰富。
例如还是利用前面提到的花朵分类的测试数据,分别对3种花在不同特征维度上进行分析。
2. 分类数据可视化
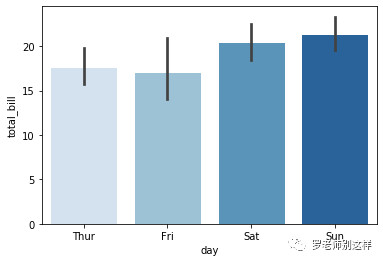
统计图:这应该是对分类数据最常见的表达方式,统计图主要反映的是一些统计值,例如求和、计数、平均数等,用于了解数据所代表的业务整体情况,在总结汇报中会经常使用,但无法帮助阅读者了解更多细节。
柱状图、折线图等形式都可以反映这类数据,例如下图反映了一家餐厅每天的平均客单价情况。
散点图:散点图可用于反映分类数据内的分布情况,例如还是该餐厅的经营数据,利用散点图可以看出客单价的分布情况,每一个点代表了一个真实订单。
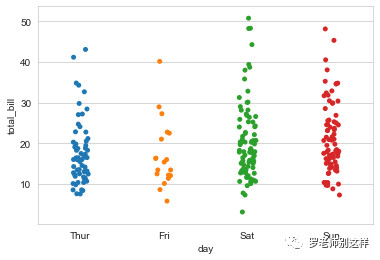
在该图的基础上,还可以再根据特定的某一参数在散点内进行分类,例如下图对付款的消费者进行了性别区分。
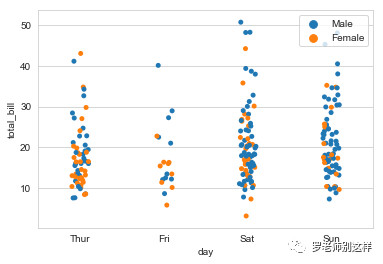
在分析特定类别时,将类别内的子类拆分显示,视觉表达效果更明确。例如下图重点观察周五和周六两天不同性别消费者的消费金额数据。
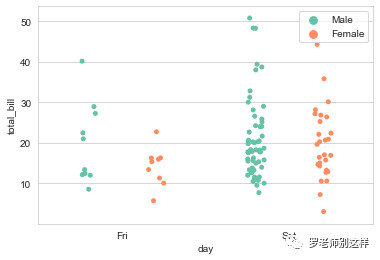
箱型图:又称作盒须图,每一个分类是一个箱子,箱型图在观察数据分布和测量统计数据上有重要意义。
箱型图的构成要素较多,信息量丰富,导致初看起来比较麻烦,但确实能反映很多问题。先介绍下箱型图中的重点要素:
- 中位数(Q2):首先要知道箱型图中的数据也是从小到大排序的,中位数即二分之一分位数;
- 下四分位数(Q1):即数据由小到大排列后,在1/4节点处的数;
- 上四分位数(Q3):即数据由小到大排列后,在3/4节点处的数;
- 四分位距(IQR):即Q3-Q1的差,在图中就是箱子的高度;
- 上限:是容许范围内的最大值,通常为Q3+1.5*IQR;
- 下限:是容许范围内的最小值,通常为Q1-1.5*IQR;
- 内限:即图中的上限和下限,在内限中的数据是正常值,在内限外的数据可以认为是异常值(注意上篇提到的,异常值不代表就是错误的值);
- 外限:外限通常代表Q3+3*IQR处和Q1-3*IQR处,外限一般不会在图中画出,除非需要单独分析以内外限分隔的数据。处于内外限之间的值被看作是温和的异常值,处于外限之外的值被看作是极端的异常值。
下图是一个简单的箱型图示例。

箱型图可以直观的识别数据中的异常值,还可以观察整体数据集中趋势、偏态、尾重等重要信息。下图还是以前面餐厅的经营数据为例,利用箱型图既能观察客单价的分布情况,还能根据需求展现相关统计值,比散点图直观了不少,一些重点信息得到了直接呈现。
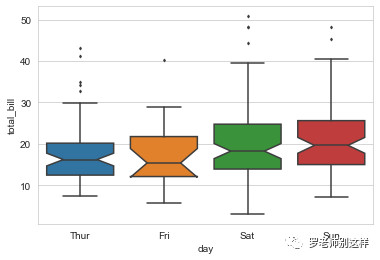
箱型图同样可以在单个分类内再区分子类,例如我们还是用性别来区分。
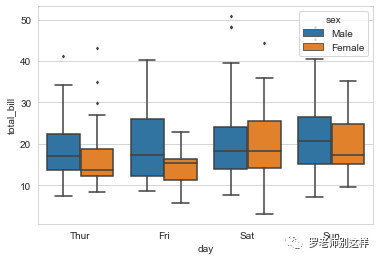
在箱型图的基础上,还可能衍生出LV图,或者小提琴图的变种,以适用于一些更有针对性的场景,这里就不多介绍了,有兴趣的同学可以自己百度。
3. 线性关系数据可视化
在前面已经讲解过了通过线性回归去寻找变量间的线性关系,现在补充一下同时对不同分类进行线性回归并进行对比的方式。
仍以上述餐厅经营数据为例,我们试图寻找账单金额和小费之间是否存在线性相关,如果还想同时观察不同性别消费者的表现差异,可针对不同性别消费者的数据进行回归分析。
从结果上看,首先账单金额和小费金额之间是存在正相关的,而性别差异对该线性相关的影响似乎不大。
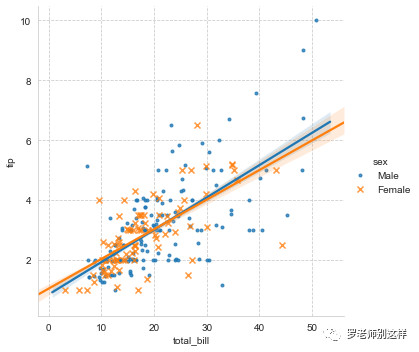
有没有更高效的展现方式呢?
回想下前面介绍的散点矩阵图,其实矩阵的思想可以用在很多地方,在这里自然也是适用的。
下图依然以性别作为分类,但上下两行代表了另一个属性:消费者是否吸烟,每列代表了每一天的数据情况。且不考虑数据和结论是否正确,似乎周六用餐的男性倾向于给更多的小费,不吸烟者尤甚(可能周六约会的人比较多,通过付更多小费能给另一半留下更好的印象)。
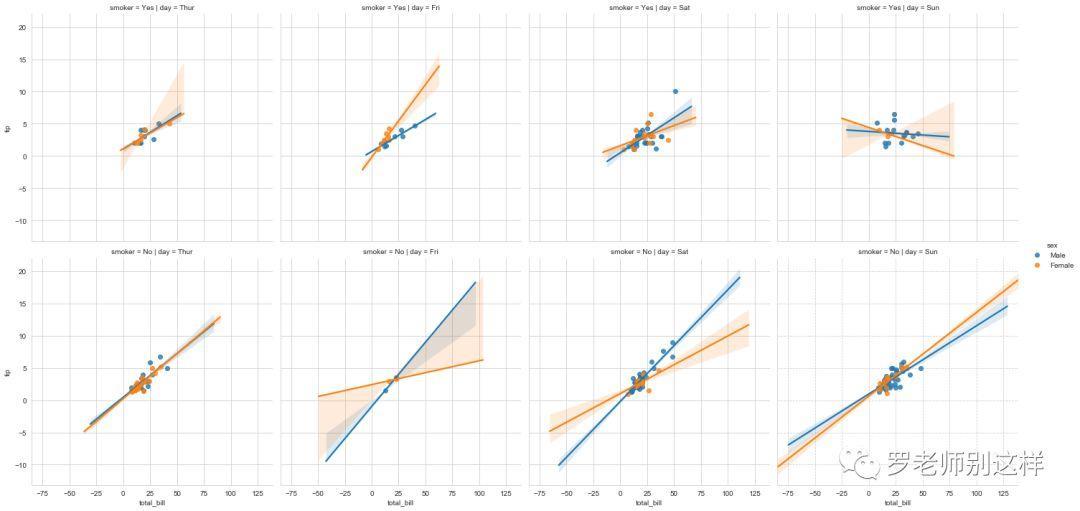
到这里本文的内容基本讲述完了,最后再附一个热力图的例子,热力图主要用于报告中加强阅读者对数据变化或聚集情况的感受。
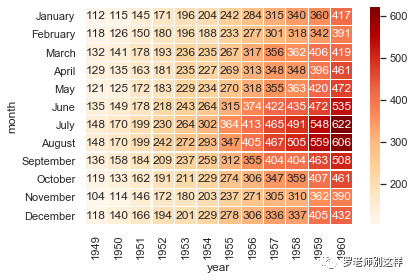
例如下图反映了从1949~1960年间某航班每月的旅客数量,可以得出结论旅客数基本逐年增长,特别在1956年后增长迅速,同时每年的夏季是出行的高峰期。
总结
本篇介绍了数据分析工作的后2步:算法建模和数据表达。
在算法建模中,可利用一系列的AI算法帮助我们进行回归、聚类和分类的工作,让我们有能力挖掘数据底层隐藏的价值。而掌握简单的线性回归算法、K-Means算法、KNN算法,已经能让你的数据分析结果深入一个层次。
在对数据分析结果的表达中,要根据表达目的选择合适的展现形式,包括反映分布情况、分类对比情况、数据相关性情况和构成情况等。
图表本身是工具,没有绝对的优劣之分,只是在不同表达目的下有不同的合适程度。就如不同的刀具对应不同的食材,砍刀最适合砍骨头,可并不代表它就完全不能用来切菜。所以我们也要根据实际情况进行选择,有时候甚至要多次比对挑出最好的展现方式。
文中重点介绍了表达分布数据的直方图、密度图(单维度/多维度)、散点图(矩阵),表达分类数据的统计图(柱状图/折线图)、散点图、箱型图,以及表达相关性数据的线性相关图(矩阵)和增强数据变化视觉效果的热力图,希望对大家日后的工作有启发和帮助。
其实写这篇文章最初的目的是概括数据分析的流程,并介绍这条线上某些具有代表性的点,让大家有全局的认识,因此不可能通过一篇文章便讲解清楚具体如何实操。
事实上,这里的每一步都可以单独写很多内容。可这些内容,只要你需要,在网上都能查到,比我写的要专业多了。所以,本文更希望是能提供作为一个系统的价值,帮助你把点串成线。
也许你看完后会觉得在面对一堆数据时仍不知道如何下手,绘制图表时仍犹豫如何展示,这很正常。因为数据分析的能力不是靠学习来提升的,而是训练,相信这个道理大家都懂。
文章、书本或课程都只是帮你导航的工具,为你指出正确的方向,避免走弯路。
但路还是得自己走。
作者:Rowan;公众号:罗老师别这样
本文由 @Rowan 原创发布于人人都是产品经理,未经许可,禁止转载
题图来自 Unsplash,基于 CC0 协议







