推荐算法改版前的AB测试 | 实验设计

编辑导语：所谓推荐算法就是利用用户的一些行为，通过一些数学算法，推测出用户可能喜欢的东西；如今很多软件都有这样的操作，对于此系统的设计也会进行测试；本文作者分享了关于推荐算法改版前的AB测试，我们一起来看一下。

一、实验背景及目的

1. 实验背景

某商城，搭建了以个性化推荐系统为核心的“猜你喜欢”功能；功能上线后，发现推荐的准确率（用户进入物品详情页定义为判断真正的正样本）较低；对此，数据分析师优化了推荐模型。

2. 实验目的

在新的推荐模型上线前，进行AB测试，以此判断新模型是否能够显著提升推荐的准确率。

二、AB测试说明及测试流程

1. AB测试定义

AB测试是为明确某个问题，制作两个（A/B）或多个（A/B/n）版本，在同一时间维度，分别让组成成分相同（相似）的访客群组（目标人群）随机的访问这些版本，收集各群组的用户体验数据和业务数据；最后分析、评估出最好版本，正式采用。

2. AB测试的特点

• 先验性： A/B测试能够先于上线，得出结论；不再需要先将版本发布，再通过数据验证效果，从而一定程度上减少改版带来的风险。
• 并行性： A/B测试是将两个或以上的方案同时在线试验，这样做的好处在于保证了每个版本对应的时间环境、数据环境保持一致，便于更加科学客观地对比优劣。
• 科学性： 如果能保证流量分配的科学性，将相似特征的用户均匀的分配到试验组中，就可以避免出现数据偏差，使得试验的结果更有代表性。

3. 应用场景

1）产品UI

不同行业的产品需要不同的风格，同时还要与企业的品牌相得益彰。利用A/B 测试优化UI能给用户带来更好的交互体验和视觉感受。

2）文案内容

顾名思义是指用户阅读到的文字内容——小到图片配文和按钮文字，大到文章标题甚至版块主题；这些部分都可以尝试变换文案内容，测试不同方案的数据效果。

3）页面布局

有些时候，可能根本不需要对产品的UI或是文案内容作出调整，只是在布局排版上的改变，就可以出现增长的效果。

4）产品功能

想给产品增加一个新功能，可是很难确定是否能达到用户的预期，如果盲目上线，可能会造成一些损失；使用A/B 测试，对你的用户真正负责；例如，社交类产品在付费查看照片的新功能正式上线前，需要进行A/B 测试，以验证功能的使用情况和效果。

5）算法/算法

包括基于内容的推荐算法（根据用户的历史记录推荐相似内容）、基于协同过滤的推荐算法（根据有相似兴趣用户的行为推荐相关内容）、基于关联规则的推荐算法（根据商品/内容本身的相关性给用户推荐）；算法优化迭代前，需要真实的数据进行测试。

4. 实验流程

三、实验设计

1. 假设检验的基本概念

统计假设：是对总体参数(包括总体均值μ等)的具体数值所作的陈述。

原假设：是试验者想收集证据予以反对的假设 ,又称“零假设”，记为 H0。

备择假设：也称“研究假设”，是试验者想收集证据予以支持的假设，记为 H1。

双侧检验与单侧检验：如果备择假设没有特定的方向性，并含有符号“=”，这样的称为双侧检验；如果备择假设具有特定的方向性，并含有符号 “>” 或 “<” 的假设检验，称为单侧检验。

临界值：是指在原假设为真的条件下，样本数据拒绝原假设这样一个事件发生的概率。

第 I 类错误(弃真错误)：原假设为真时拒绝原假设；第 I 类错误的概率记为 α(alpha)。

第 II 类错误(取伪错误)：原假设为假时未拒绝原假设。第 II 类错误的概率记为 β(Beta)。

2. 实验原理说明

先认定原假设成立，然后在事先给定的显著性水平下，构造一个小概率事件，根据抽样结果观察小概率事件是否发生；若小概率事件发生，则拒绝原假设，否则接受原假设。

3. 实验流程设计

1） 提出假设

本次AB测试，目的是希望提升猜你喜欢功能的推荐效果。所以选取推荐系统的准确率，作为优化指标。

准确率表示预测为正的样本中，真正的正样本的比例。公式如下：

R（u）是根据用户在训练集上的行为给用户作出的推荐列表，而T（u）是用户在测试集上的行为列表。

最简单的例子：例如推荐系统给用户推荐了10件物品，用户进入物品详情页定义为判断真正的正样本的行为，用户进入了其中3件物品的详情页，则此时准确率=3/10=30%。

假设我们认为，如果新的推荐算法，比原推荐算法，显著高于5%以上，则可将新推荐算法发布至生产环境。

此时我们可以得到假设：

原假设H0：π2-π1≤5%

备择假设H1：π2-π1＞5%

2）确定显著性水平α

本次实验中，α 值设定 0.05（5%），这是假设检验中最常用的小概率标准值；表示原假设为真时，拒绝原假设的概率。

3）确定临界值

临界值是显著性水平对应的标准正态分布的分位数，显著性水平0.05的情况下，单侧检验对应的标准正态分布的分位数是1.645，双侧检验的标准正态分布的分位数为1.96。

4）收集实验数据，得出结论

由样本值求得检验统计量的优化指标的数值。若观察值在拒绝域内，则拒绝原假设H0，否则接受原假设H1。

四、开始测试并分析数据

定义新推荐算法的准确率为π1，新推荐算法的准确率为π2。

Ho：π1-π2≤5%

H1：π1-π2＞5%

实验目标人群：从进入商城，且使用了“为你推荐”功能的用户流量（UV）中，随机抽取5%，作为实验目标人群；其中的50%为实验组，50%为对照组。

实验时间：1周

假设检验方式：

不同的AB测试场景，适用于不同的检验方式，如上图所示。

本次AB测试，由于两个推荐系统版本是独立的，且样本数足够大，认为满足正态分布。

根据HO、H1的假设，可判断本次检验为两个独立样本的总体均值的单侧检验，且总体方差未知，需要用样本方差代替总体方差。

此时计算统计量公式为：

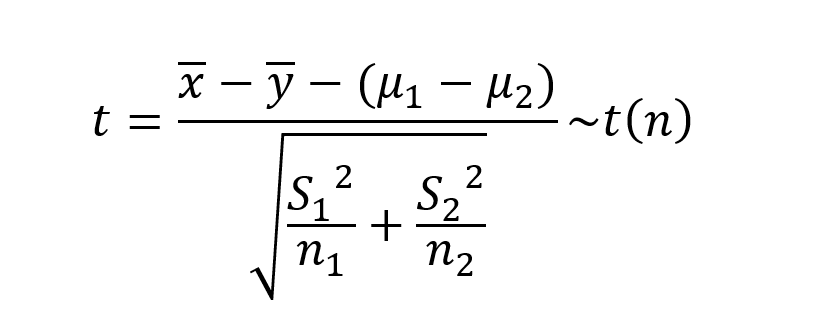
显著性水平：0.05。

临界值：在显著性水平为0.05时，单侧检验的临界值Zα为1.645。

实验数据(为方便计算）：实验一周后，有10000用户，使用新推荐算法，准确率的平均值为41%，标准差为20%；有10000用户，使用原推荐算法，准确率的平均值为35%，标准差为10%。此时新算法的准确率定义为x，则x的平均值=41%，原算法的推荐率定义为y，则y的平均值=35%。

计算检验统计量：

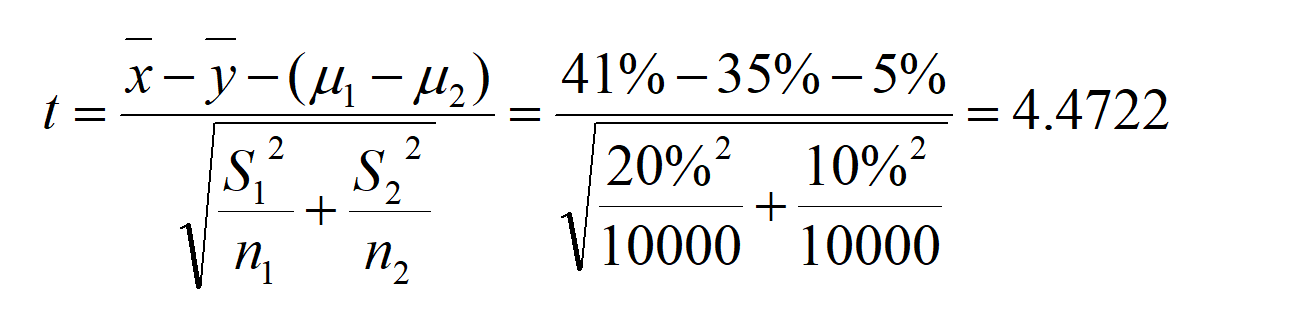
检验结果：统计量Z=4.4722，临界值Zα=1.645.由于统计量的值大于临界值而落入拒绝域内，所以拒绝原假设H0，认为新推荐算法的准确率，比原推荐算法显著高出5%，新版本算法可发布至生产环境。

 

本文由 @16哥 原创发布于人人都是产品经理，未经许可，禁止转载。

题图来自 unsplash，基于 CC0 协议